4.2: Engineering Ordinal Features

Ordinal feature, just like the categorical feature has multiple categories. The difference between the both type of feature is that in the case of ordinal feature, categories follow a specific order. For example, an ordinal feature 'age group' can have the age of individuals recorded as categories such as 'kid', 'teenager', 'adult', and 'elderly'. These categories are reflective of the age of individuals from lower to higher value incrementally. In this case, the 'age group' can be considered an ordinal feature. Let s discuss the different types of encoding possible for ordinal features.

Let's consider the ordinal feature 'income' in the coupon recommendation data set. It has 9 levels, starting from 0 to more than 100000. Each category is a range with lower and upper ranges. The difference between the upper and lower ranges of each category is 12499. The difference between the lower range of the next category and the upper range of the previous category is 1.

Just like categorical features, ordinal features should be presented as encodings.

4.2.1    Rank Encoding

This is the most simplistic feature encoding for ordinal features. We rank categories in such a way that the category of least value is given a value of 1 and for other categories, we incrementally increase the label by 1. In the example given for 'income', the category ''Less than $12500'' will be given value as 1, for '$12500 - $24999' it will be 2, and so on.

Below is a snapshot of the rank-encoded representation of the income feature.

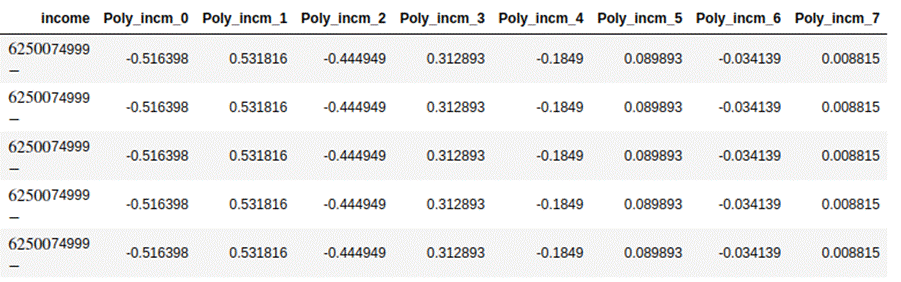
4.2.2    Polynomial Encoding

It searches for 3 different types of trends in the feature, based on which it creates contrast encodings. It fits a regression line using mean, quadratic parabola, and a cubic term to produce linear, quadratic, and cubic encodings. If the ordinal feature has N number of categories, polynomial encodings produce N-1 polynomial encodings. Below is a snapshot of polynomial encoded features for  income .

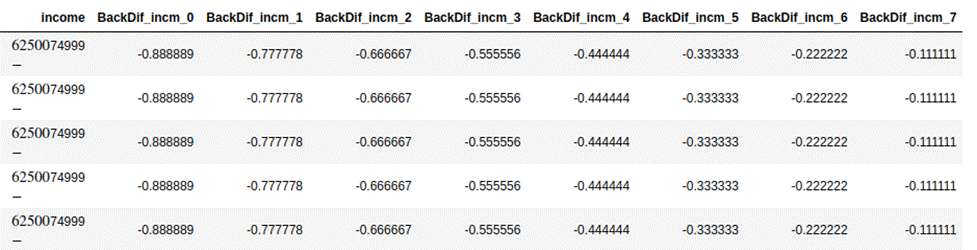
4.2.3    Backward Difference Encoding

In this method, the mean of the dependent variable for one level of the categorical variable is compared to the mean of the dependent variable for the prior adjacent level. It produces N-1 encoded features for N categories in an ordinal feature. Below is a snapshot of backward difference encoding for  income .