8.5: Particle Swarm Optimization

The particle swarm optimization (PSO) is an optimization algorithm that tries to iteratively improve candidate solutions. Individual candidate solutions are known as particles. The population of all candidate solutions, which comprises all particle candidate solutions, is called a swarm. It tries to move the candidate particles in the search space using the position of the particle and velocity. Each particle tries to move toward the best-known position, based on the better position found by the particle itself and also the better position found by other particles collectively in the swarm. This helps the swarm to collectively move towards better solutions. This process is iteratively repeated to find the best possible solution.

It is inspired by the collective behavior of animals such as birds. For example, a swarm of birds is a swarm of insects. Let's take the example of a flock of birds. A flock of birds flies to find a place where food availability is maximum and the presence of predators is minimum. If a bird has to change its direction from its flock, it does so by changing its direction and redirecting its force in the new direction. Birds also share information amongst themselves about changes in direction. Once the best place is found by one of the swarm s members, the rest of the birds follow the direction of the first bird to change direction. By sharing information, birds of the flock together have a greater chance of survival than if they had to survive alone.

Let's try to understand the mathematics behind PSO. X is an n-dimensional vector that tries to optimize a given objective function f(X). Here n is the number of factors or variables that have an impact on the outcome. For birds, it can be the longitude and latitude of the place where they want to land. For P particles in the swarm that goes through the  t  number of iterations, the position vector can be represented as X^t_i = (x_i1 x_i2 x_i3 x_in)^T. The velocity vector can be represented as V^t_i = (v_i1 v_i2 v_i3 v_in)^T. Individual particles are denoted as  i  and have values from 1 till P. Position and velocity vectors are updated through j dimensions with the help of the below 2 equations, where j has values from 1 till n.

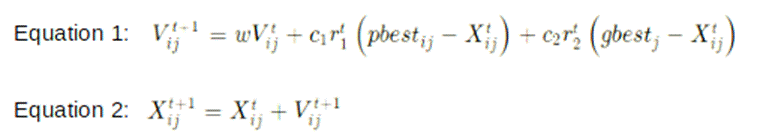
Equation 1 is used for updating the velocity of the particles, whereas equation 2 is used for changing the particle's positions. In the above two equations, c1 and c2 are positive acceleration constants. The constant c1 relates to previous learning by the same particle, whereas the constant c2 is a social learning constant. r1 and r2 are random values between 0 and 1 and help PSO to avoid getting stuck at local minima/maxima and increase the likelihood of finding global minima/maxima. w is inertia weight constant and is a positive number. It helps update velocity by multiplying the previous velocity and the weight constant. If it is kept above 0 but less than 1, the swarm will be able to explore more solutions in the searching domain and have more chances of getting global minima. Although, as a consequence, it can increase the computation time.

The pbest represents individual learning, whereas gbest represents global learning. If the pbest term (pbest_ij - X_ij^t) increases, it can help individual i^th particles towards the best possible position. If the gbest term (gbest_j - X_ij^t) increases, it can help find the global best of the swarm.

Figure 8.5.1 below is the flowchart of PSO ^[3].

Figure 8.5.1: Flowchart of particle swarm optimization

We can use the function ParticleSwarmOptimization in the feature selection object fsObj for performing particle swarm optimization. Below is how the syntax will look like.

best_columns = fsObj.ParticleSwarmOptimization(iterations = 25,
                                               swarmSize = 75,
                                               run_time=1200)

In this syntax example, we have executed particle swarm optimization for 25 iterations. Within each iteration, we have swarm size of 75. Execution time limit is set for 1200 minutes.