5.2: SHAP

Shapley additive explanation (SHAP)^[1] method can help us detect feature interactions. SHAP is a model explanation technique. For a specific data point, it can explain the extent of importance a feature has on a model for the data point. It uses game theory to quantify the contribution of each feature. Positive and negative SHAP values represent their impact in increasing or decreasing the prediction outcome. SHAP can be extended to find interaction amongst features. It does so by ascertaining the impact of the main effect and interaction effect.

There are three steps for finding the interaction effect using SHAP. The first step is to create a model with available features. The second step is to calculate interaction values using the SHAP python package, for each record, using the model. The result from SHAP will be in the form of a matrix, which has interaction amongst all features, for each record. The third step is to aggregate interaction values across all records to get overall interaction across features. If the number of features is a handful, we can visually inspect to understand the overall feature interaction of features. If the number of features is numerous, we can instead do mathematical aggregation, such as mean value to finalize the extent of interaction.

There are a few caveats with using SHAP feature interaction.

1) The interactions identified by SHAP will be as good as the model. If the model is not of good performance, interaction effects detected by SHAP will not be reliable.

2) Calculating SHAP interaction values is computationally expensive.

3) There is no fixed cutoff value of the SHAP interaction value. For some interactions, it can be 0 or very close to 0. If a cutoff is indeed needed to be established, it will be the discretion of the analyst. We put a cutoff of 0.1 for the sake of convenience. We will remove interactions for which SHAP mean score is less than 0.1.

4) The method shap_interaction_values is available for TreeExplainer in SHAP python library. It can only be used for tree-based bagging and boosting technique for obtaining interactions. It cannot be used for models which do not use a decision tree at its core, such as linear regression, or logistic regression. etc.

One advantage of using SHAP for interaction effects is that it can be used for both regression and classification. This is unlike the interaction plot method discussed earlier, which is useful only for regression.

Let s use this method for finding the interaction effect in the coupon recommendation dataset and car sales dataset.

5.2.1    Car Sales

For the car sales dataset, we ran the experiment across all cross-validation training samples. Each cross-validation has a set of interactions discovered by SHAP. To avoid overfitting, we will consider only those interactions which are present across all cross-validations. We shortlisted 374 interactions that were present in all 5 cross-validation samples and where the SHAP value was greater than or equal to 0.1. Also, SHAP values for the 374 features were obtained by averaging across 5 cross-validations. By looking at the interactions discovered by SHAP, we can infer that it was able to detect interaction only amongst higher-order features. Figure 5.2.1a is the plot for the bottom 5 interactions.

 

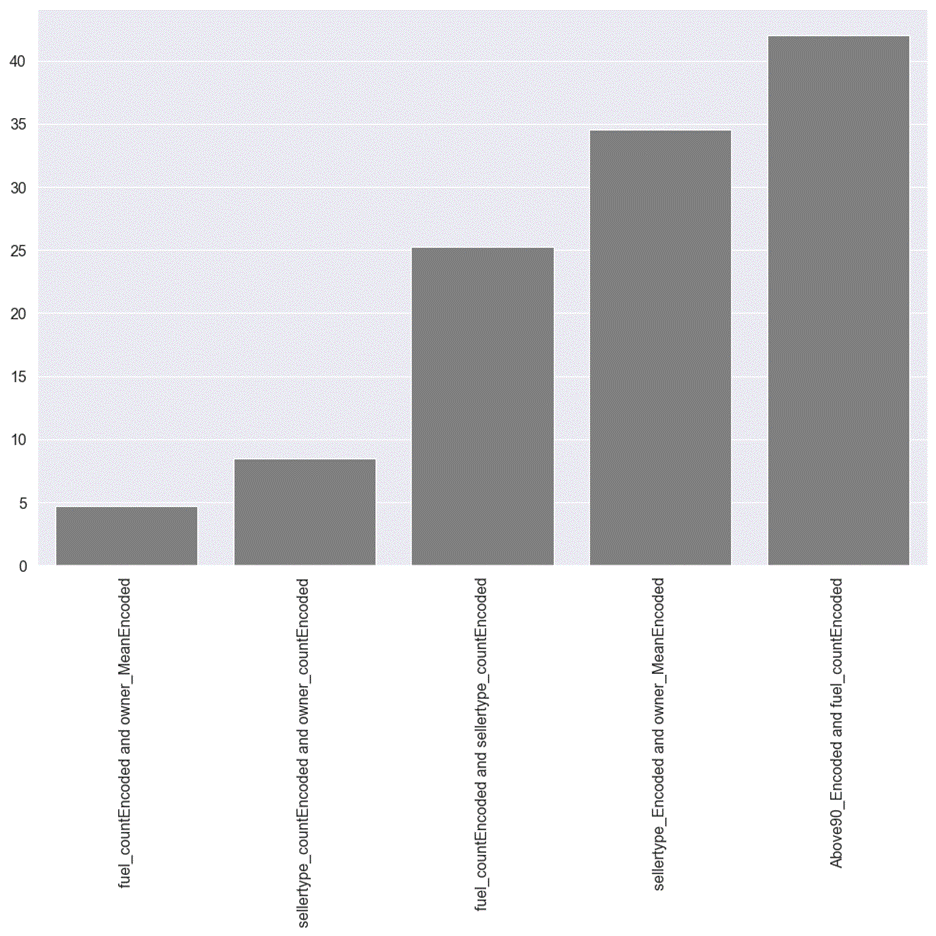
Figure 5.2.1a Bottom 5 interactions

Higher-order features for fuel and owner have the lowest degree of interaction effect. For fuel, count encoding of different categories is a numerical variable. It has a weak interaction with the mean encoding for dependent variable for the owner feature. The rest of the bottom 5 interaction effects are amongst higher order features and none of these are original features.

Now let s understand the top 5 interaction effects in figure 5.2.1b.

Figure 5.2.1b Top 5 interactions

Label encoding of 2 features namely torque and Above90 have the highest degree of interaction effect. Since both the features are categorical, we can do a simple concatenation between the two features to obtain an interaction effect feature. For the rest of the interactions in the top 5, all the features are label-encoded feature of a categorical feature. For such interaction between categorical encoded features and other higher-order features, we can simply perform concatenation between two features to obtain interaction effect feature.

5.2.2    Coupon Recommendation

Now let s look at the coupon recommendation dataset. The interaction was detected amongst higher order encoded features of categorical features. Although the magnitude of the interaction effect is small, there were 6 interaction effects detected in this dataset. These interaction effects were present across all cross-validation samples. These are shown in figure 5.2.2.

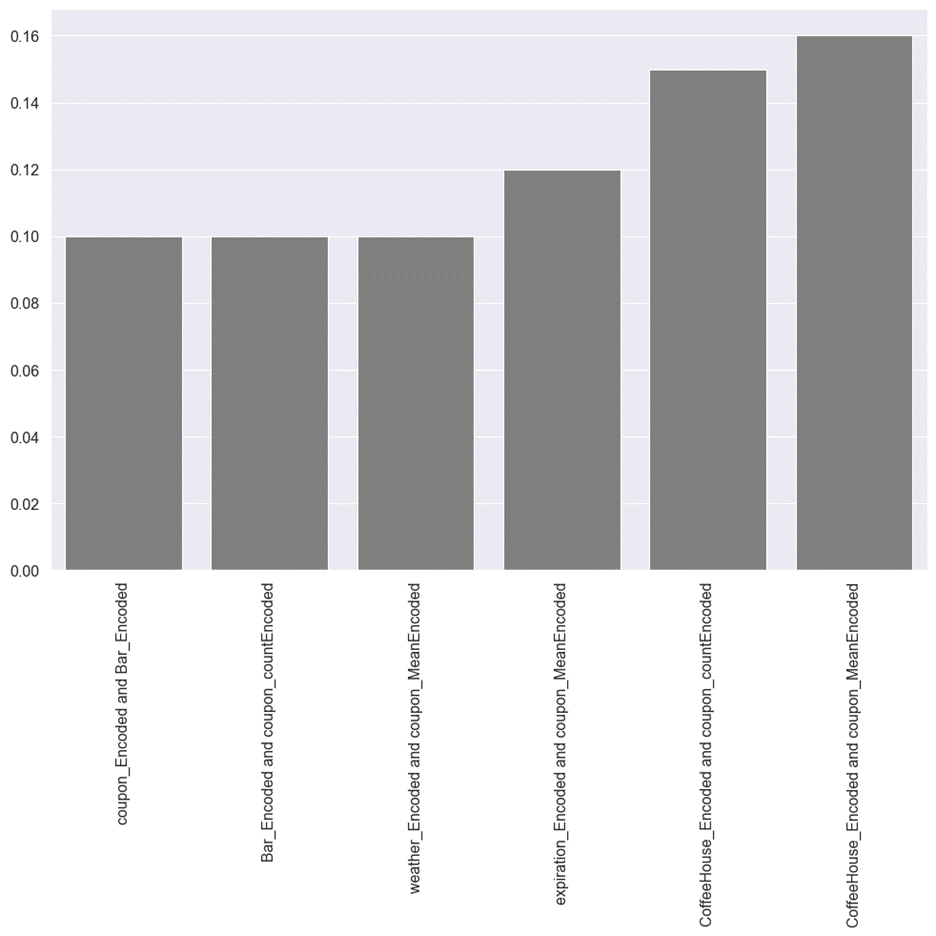
Figure 5.2.2 Interactions detected for coupon recommendation dataset

The smallest degree of interaction was detected between label encoding feature for bar, and label encoding for the type of coupon. Both features are numerical. For the rest of the detected interactions, at least one feature is label-encoded features of a categorical feature, while the other feature is a count or mean encoded feature. The only way to create interaction feature between these two types of features is by creating dummy variables of the label encoded feature and multiply it with the numerical feature.

The next step will be to create new categorical or numerical features from these features. For newly created categorical features, these can't be used directly. To be able to use these features, we will need to further create higher order features from these categorical interaction effect features.

For the rest of the datasets, the feature matrix is huge. It is computationally very expensive to detect interaction effects through SHAP. Also, most of the features are higher order features for either date of check-in, revenue, and booking patterns. Hence, there is a chance that very few interaction effects could be detected which are meaningful and could be explained to laymen.