9.3: Explanation Techniques

Linear regression, logistic regression, and decision tree discussed previously, have inherent properties available to explain model behavior. Many other non-linear and complex algorithms do not have any such available property to explain model behavior. For any model to be of practical use, it is helpful to have some type of explanation of the model. The explanation is sought for both the overall model behavior and individual predictions. These explanation techniques can be applied to any machine learning technique, including explainable models.

In the following sections, 9.3.1 and 9.3.2, we will try to explain the models and individual predictions for the hotel total rooms booking predictions dataset and hotel bookings cancellations dataset. After finding the best model, the model should be trained on the whole dataset, including validation, and external test data. If, however, the performance of the model worsens, we should revert to the original training data used within the cross-validation training sample. For this chapter, we need data points to explain the model prediction. We will only keep external test data and will train the model on training and validation data.

9.3.1    Explaining Overall Model

There are methods available to explain the model as a whole. It can explain the collective nature of the model.

9.3.1.1 Partial Dependence Plot

It is otherwise known as PDP. It is performed at the feature level, one feature at a time. A predefined test data is used for PDP. For the feature under exploration, each value is processed individually. If the feature under observation is M and it has n rows, then from M₁ to M_n iteratively model predictions are obtained. In each iteration, all the values in feature M are replaced with M_i in the test data matrix, while values for all other features are kept constant. In the next step, predicted values are obtained and averaged for M_i. Once done, averaged predictions and different values of the feature are plotted together to understand the relationship between the target and the feature.

It can identify if the relationship between the feature and the dependent variable is linear, monotonic, or more complex. More the degree of change in prediction as against the change in the feature, the more important the feature. It suffers from a few limitations. One such limitation is that it assumes that there is no correlation between different features and ignores possible feature interactions.

Let us now look at partial dependence plot in figure 9.3.1.1 for one of the features in the hotel room booking dataset  CumulativeNumberOfRoomsNet_Quartile_Encoded . We have used Lightgbm model for the plot.

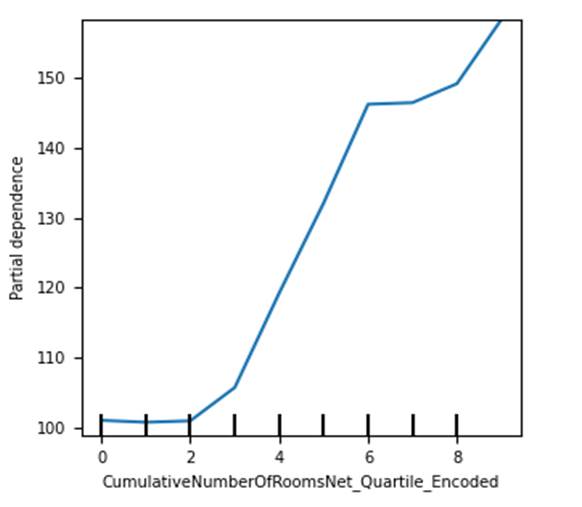
Figure 9.3.1.1 partial dependence plot of Lightgbm regression model for the hotel total room booking dataset for  CumulativeNumberOfRoomsNet_Quartile_Encoded  feature.

We can see that relationship of the feature with the dependent variable is nearly linear in nature.

9.3.1.2 Accumulated Local Effects Plot

It is abbreviated as ALE plot. It overcomes a major disadvantage of a partial dependence plot and can work even when features are correlated.

It studies the effect of the feature at a certain level against average predictions. At a specific value for a feature, it will suggest to what extent prediction is higher or lower than average prediction. It takes the quantile distribution of features or specified intervals within the domain of the given feature to define intervals. This enables comparison among different features.

Now let us now look at the ALE plot in figure 9.3.1.2 for the same scenario we discussed earlier, for the hotel room booking dataset.

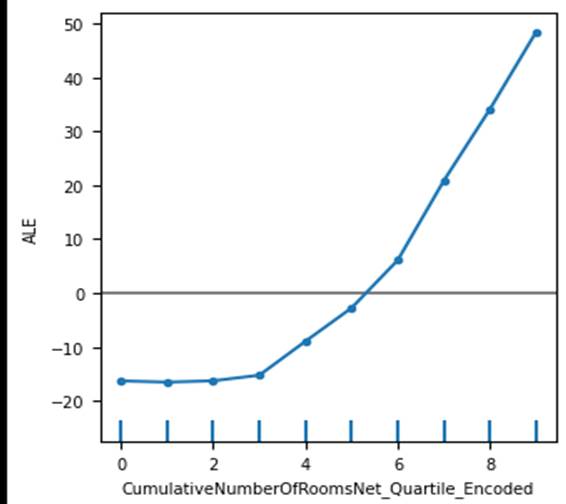
Figure 9.3.1.2 accumulated local effects plot of Lightgbm regression model for the hotel total room booking dataset for  CumulativeNumberOfRoomsNet_Quartile_Encoded  feature.

As it considers quantile distributions, plot is smooth at the top end. Very high values that stands out in PDP is smoothened for the ACE plot. It looks more stable and easier to interpret, in comparison to partial dependence plot.

9.3.1.3 Permutation Feature Importance

This method uses prediction error as a marker of feature importance. The List of values from the feature is selected based on permutation and shuffling. The Prediction error is obtained for permuted values. If prediction error increases for permuted shuffled values of a feature, it is considered important.

This is done by obtaining original errors for specific test data as the first step. In the second step, for each feature permutation error is obtained by selecting feature values based on shuffling and permutation while keeping the value of other features constant. The permutation feature importance quotient for each feature is calculated as the original error divided by the permutation error of the feature. Finally, the permutation feature importance quotient is sorted in descending order for all features together to obtain the most and least important features in descending order.

Although it takes into account all types of feature interactions amongst different features, if some features are correlated, it can decrease the importance of correlated features.

9.3.1.4 Surrogate Model

Through a surrogate and easy-to-explain model such as linear or logistic regression, we can try to explain a black-box model. For being able to do this, 3 datasets are needed. The first dataset is black-box model training data, which is used for training the black-box model. The second dataset is surrogate model training data and the third dataset is test data.

After the black-box model is trained using black-box model training data, features from surrogate training data are used and predicted values are obtained for surrogate training data and used as a dependent variable of the surrogate model. The surrogate model is trained using predicted labels from the black-box model as the dependent variable and features from the surrogate training dataset. Finally, both the black-box model and surrogate model are used for generating predictions for test data. If the performance of the black-box model and surrogate model is similar and the R-square of the surrogate model is acceptable, then the surrogate model is used for explaining the black-box model.

9.3.2    Explaining Individual Predictions

Understanding how the model performs through the explanation of the overall model is useful. There are methods available for explaining individual predictions from the model as well. These techniques can be useful when we have to probe the root cause behind certain predicted values from the model at an individual level.

9.3.2.1 Individual Conditional Expectation Plots

It is otherwise known as the ICE plot. It is related to the partial dependence plot method. However, it differs in the aspect that plots are generated for individual values instead of averages. One line in ICE represents one sample. It can help us understand the pattern of change in prediction concerning change in a feature.

Figure 9.3.2.1 has the ICE plot for the  CumulativeNumberOfRoomsNet_Quartile_Encoded  discussed earlier. We can see that the linear relationship explored between the feature and dependent variable is not always true. In many cases it is polynomial. As we can see the total rooms sometimes increase and then decrease between different quartiles of the feature.

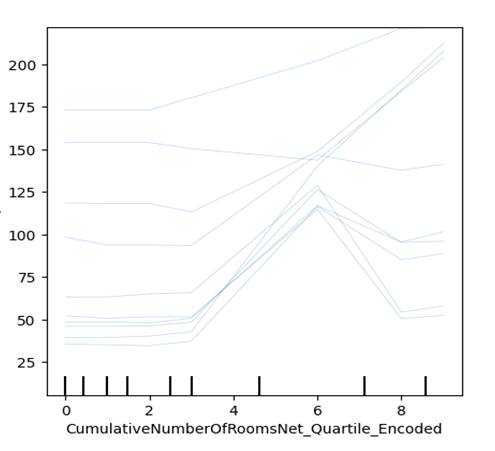
Figure 9.3.2.1 Individual Conditional Expectation plot of Lightgbm regression model for the hotel total room booking dataset for the first 10 rows of external test data, for the feature  CumulativeNumberOfRoomsNet_Quartile_Encoded 

9.3.2.2 Local interpretable model-agnostic explanations

It is otherwise known as LIME. It uses an explainable model to explain individual predictions of a black-box model. To explain a specific prediction from the black-box model, a perturbed sample dataset is created. To explain a specific predicted value from the black-box model, all the values from the feature matrix are taken and randomly changed for different features. A new dataset is created from this exercise. For this dataset, prediction from the black-box model is obtained.

Perturbed samples are weighted based on proximity to the original feature values which we are trying to explain. The predicted value from the black-box model is used as the dependent variable and weighted perturbed feature values as features for training an explainable model.

Finally, the instance we were trying to explain from the black-box model is explained through an explainable model.

Figure 9.3.2.2 displays the LIME plot of Lightgbm regression model. We have used 4th row of external test data from the hotel total room booking dataset.

Figure 9.3.2.2 LIME plot of Lightgbm regression model for the hotel total room booking dataset for the 4th row of external test data.

This plot has 3 subplots. First subplot has the predicted values and third subplot has actual feature names and values. The second subplot has a negative and positive relationship indicator against each feature. For example, for the  DayofWeek_Encoded  feature, total rooms increase in demand for days that are farther from Monday. Similarly, for the  AdjustedLeadTimeCumulativeNumberOfRoomsNet_Quartile_Encoded  feature, it has a negative relationship with total room demand. This is the interaction between lead time and the net number of rooms quartile feature. The second part of the plot also suggests the current value for the feature, against a threshold set by the model. For example, the  DayOfMonth_Encoded  feature, has a negative relationship with the total rooms sold for a check-in date. I.e. Total number of rooms is sold more towards the beginning of the month, and then gradually decreases as the month passes. Here the value is 20, which is higher than the set threshold of 15, and the check-in date for which the model has predicted is farther in the month.

9.3.2.3 Counterfactual Model Explanations

The counterfactual model explanation is a way of explaining a model where the smallest change in a feature is compared against a noticeable change in the predictable outcome. To understand "Noticeable outcome", let's take an example of a model which predicts if someone has diabetes or not by using daily minutes of exercise, a binary-coded feature for a family history of diabetes, age, and a binary-coded feature for the stressful job. For someone who exercises for 45 minutes, with no family history of diabetes, who is 40 years old, and who has no stress job, the model prediction outcome came as non-diabetic. However, by only changing jobs as stressful, the prediction came as diabetic. In this case, the noticeable outcome is changing between the different classes of diabetic vs non-diabetic.

Similarly, let's take a regression prediction problem. We are predicting someone's income potential based on age, highest qualification, and distance from the nearest metropolis. If the age is below 30, the highest qualification is a bachelor's and distance is 200 miles, predicted income is $40000. However, if we reduce the distance from the metropolis to 10 miles, income changes to $65000. In this case, an additional income of $25000 is 62.5% more than the previous salary. It can be considered a "noticeable outcome".

This method tries to identify the smallest change to the features which will bring noticeable outcomes. However, these changed feature matrices should be similar to the original instance we are trying to explain. Minimal changes should be present in additional instances we are using to explain the original instance. These instances are used for explaining the original instance. It will be explained in the lines  if we make  x  change in  m  feature, the outcome will change noticeably , as a counterfactual.

Figure 9.3.2.3a and 9.3.2.3b has the Counterfactual plot of Lightgbm regression model for the hotel total room booking dataset. We have plotted the 4th row of external test data.

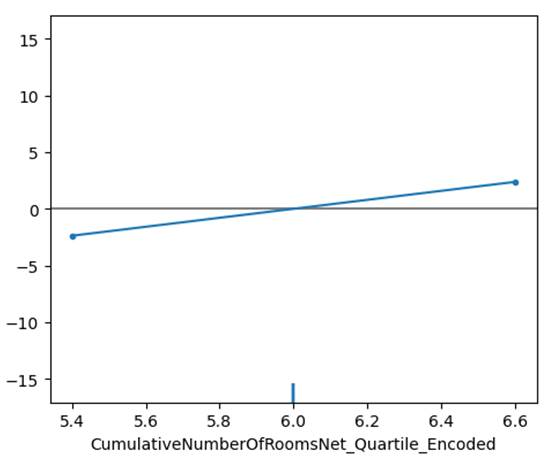
Figure 9.3.2.3a Counterfactual plot of Lightgbm regression model for the hotel total room booking dataset for the 4th row of external test data, for the feature CumulativeNumberOfRoomsNet_Quartile_Encoded feature.

Figure 9.3.2.3b Counterfactual plot of Lightgbm regression model for the hotel total room booking dataset for the 4th row of external test data, for the feature AdjustedLeadTimeCumulativeRevenueNet_Quartile_Encoded.

Previously, we have seen that the feature  CumulativeNumberOfRoomsNet_Quartile_Encoded  has the highest impact on overall model. For this instance of data, this has a relatively stable and lower contribution for the output. Even if we changed the values of the feature, the impact on outcome was marginal. In contrast, for the feature  AdjustedLeadTimeCumulativeRevenueNet_Quartile_Encoded , if we slightly changed the values, the impact on output was higher than previously thought.

9.3.2.4 SHAP

SHAP is the contribution of each feature towards the predicted outcome from the model. To calculate the SHAP value, in the first step model performance is obtained for a sample dataset. In the second step, the importance of individual features is obtained by giving different values to the model and observing whether model performance increases or decreases. It can be positive or negative. To identify the most to least impactful features, the absolute value of SHAP is considered.

We can obtain SHAP feature importance for each observation in the feature matrix. This can help us interpret the model globally by analyzing and summarizing the SHAP values in each observation for each feature.

Now let us look at the SHAP model explanation for the 4th row of external test data for Lightgbm regression in figure 9.3.2.4

 

Figure 9.3.2.4 SHAP plot of Lightgbm regression model for the hotel total room booking dataset for the 4th row of external test data.

We can see the most impactful feature is  MonthofYear_Encoded . This is followed by  DayOfWeek_Encoded . The feature  AdjustedLeadTimeCumulativeRevenueNet_Quartile_Encoded  was found to be one of the impactful features in counterfactual model explanation method. SHAP found this to be the third most impactful feature for the 4^th sample of external test data.