8.2: Genetic Algorithm

The genetic algorithm technique is an optimization technique. It is a population-based metaheuristics search algorithm, inspired by the natural phenomenon of evolution. Parents produce offspring, who inherit the strengths and abilities of both parents in the form of genes. This happens through a process called crossover. In the genetic algorithm, the crossover is carried out at one or more random cut-off points and the gene is swapped from both parents based on crossover probability. Figure 8.2.1 below illustrates the process of crossover. The cut-off point for the genes is kept in the 4th column for the parents and highlighted in red. Genes are swapped at the cut-off points and child 1 and child 2 have the swapped genes. Genes from the beginning until the cut-off point are the same as parents. From the 5th point onwards, genes are obtained from the other parents.

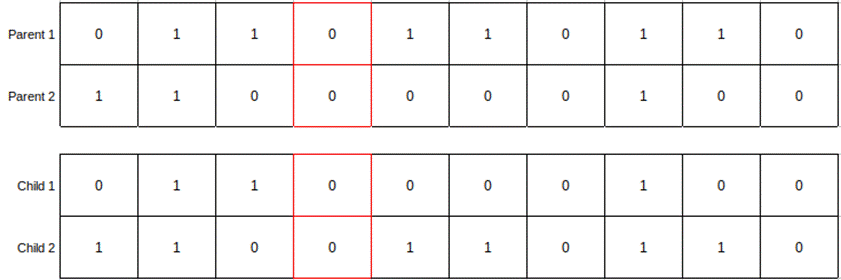
Figure 8.2.1: Crossover in genetic algorithm

There is also a likelihood of genetic mutation when a gene is passed from parents to offspring. In the case of the genetic algorithm, a mutation is introduced in the form of new patterns to randomly refresh the population. This encourages the search for unexplored feature combinations. A small probability (1% 2%) is selected for each possible feature as mutation probability. A random number is generated. If the random number is less than the mutation probability, then the feature is mutated and its status is changed. If it was originally supposed to be included, it is excluded and vice versa. Figure 8.2.2 explains the mutation process in the genetic algorithm.

Cells highlighted in red were mutated and values were changed. If the original value was 1, it was changed to 0, and vice versa.

Figure 8.2.2: Mutation in genetic algorithm

An initial set of solutions are created, called population. Each solution in the population is called a chromosome . Each chromosome has a length equal to the total number of features. Individual features are represented as binary 0/1. 0 stands for a specific feature being removed from feature space and 1 stand for the feature being included. As explained previously, through the process of crossover, a list of the best chromosomes is selected and passed through mutation. This process is repeated several times, based on how many generations are defined by the user. Imagine there are 10 features x1 to x10 and we want to try 7 solutions at a time. i.e., a population of 7. Figure 8.2.3 illustrates what the initial solution will look like for 10 features and a population of 7. Each row will be a chromosome and all chromosomes combined will be called population. Figure 8.2.4 illustrates the genetic algorithm flowchart.

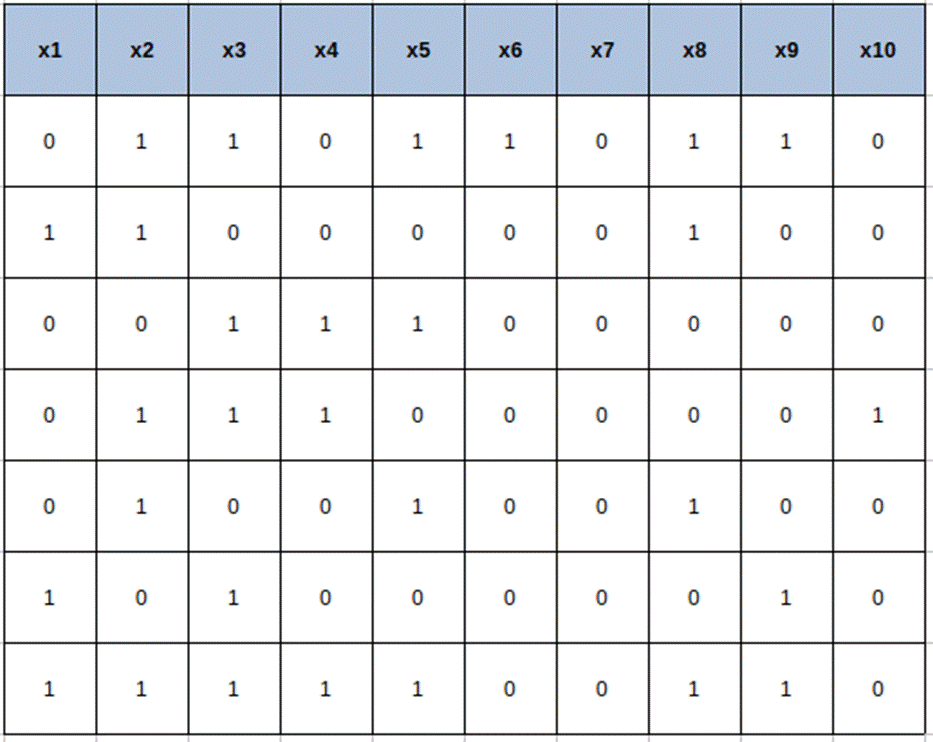
Figure 8.2.3: Solution matrix for 10 features and population of 7

 

 

 

 

Fig 8.2.4: Genetic algorithm flowchart

M: Number of generations

N: Population size

p_c: Probability of crossover

p_m: Probability of mutation

k: Number of contestants

Number of generations, population size, crossover, and mutation probability are some of the hyperparameters of genetic algorithm.

This method tries to find the best possible feature combination by searching in a computationally efficient manner. This also means it does not search for all possible combinations. As a result, the best-performing features obtained from the genetic algorithm might not be the best combination of features. If the number of features are small, the genetic algorithm can be a really useful method. However, for high dimensional data in which the number of features is numerous, the genetic algorithm might not be computationally efficient, and the resultant features obtained from the genetic algorithm might not be useful either.

We have earlier initialized a feature selection object in this chapter as fsObj = FeatureSelection. We can use the object fsObj for performing the genetic algorithm by using the GeneticAlgorithm function in the object fsObj. Below is how the syntax will look like.

best_columns = fsObj.GeneticAlgorithm(generations=20, population=75, run_time=1200)

In this syntax example, we have used 20 generations and 75 population for the genetic algorithm. We will execute genetic algorithm feature selection for 1200 minutes, i.e., 20 hours and will stop the execution after that.